Auf dieser Seite gibt es für euch Numerik / Numerische Verfahren – Mathe Abituraufgaben mit Lösungen und zwar Aufgabe C1 a und b (Sachsen 1994).
Aufgabe a)
Die Gleichung 2x – x = 3 soll graphisch gelöst werden!
Mit Hilfe des allgemeinen Iterationsverfahrens soll nun die positive Lösung der Gleichung bestimmt werden, wobei die Gleichung nach dem Exponenten x der Potenz 2x aufgelöst werden soll!
Lösung:
Für eine graphische Lösung formen wir die gegebene Gleichung 2x – x = 3 um zu
Wir betrachten nun die linke und die rechte Seite dieser Gleichung als die Terme zweier Funktionen f und g:
Mit Hilfe einer Wertetabelle – z.B. für -3 ≤ x ≤ 3 – gewinnt man schnell einige Wertepaare für diese beiden Funktionen. Zeichnen wir nun diese Funktionen in ein Koordinatensystem, so sind die x-Koordinaten der Schnittpunkte (die roten Punkte auf der x-Achse) die Lösungen unserer Gleichung:
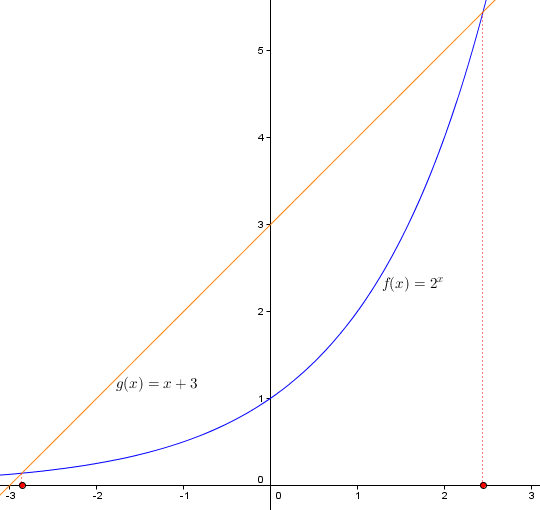
Aus der Zeichnung lesen wir die beiden Lösungen x1 ≈ -2,8 und x2 ≈ 2,4 ab.
Kommen wir nun zur numerischen Bestimmung der positiven Lösung von 2x – x = 3. Wir nehmen zunächst die geforderte Umformung vor:
2x – x = 3
2x = x + 3
x = log2(x + 3)
Wir verwenden also die Iteration
und benutzen als Startwert x0 die abgelesene Lösung 2,4. Wir brechen das Verfahren ab, sobald sich die vierte Nachkommastelle nicht mehr ändert:
x0 = 2,4
x1 = log2(2,4 + 3) = 2,43295940727611
x2 = log2(2,43295940727611 + 3) = 2,44173826785587
x3 = log2(2,44173826785587 + 3) = 2,44406756872523
x4 = log2(2,44406756872523 + 3) = 2,44468497287789
x5 = log2(2,44468497287789 + 3) = 2,4448485776447
x6 = log2(2,4448485776447 + 3) = 2,44489192785518
Hier können wir nun aufhören, da an der vierten Stelle hinter dem Komma erneut die 8 aufgetaucht ist.
Die exakte Lösung beginnt also demnach mit 2,4448… und wir setzen unsere Näherungslösung ‚auf‘ x = 2,445 und weichen damit um weniger als 10-3 von der exakten Lösung ab.
Aufgabe b)
Die Funktion f(x) = 8x3 – 55,5x + 13,75 besitzt genau eine Nullstelle im Intervall -3 ≤ x ≤ -2 und genau eine Nullstelle im Intervall 2 ≤ x ≤ 3.
Zeige, dass f im Intervall 0 ≤ x ≤ 1 genau eine Nullstelle besitzt ohne diese zu berechnen!
Bestimme im Anschluss mit Hilfe des Newton-Verfahrens die Nullstelle aus dem Intervall -3 ≤ x ≤ -2 auf zwei Nachkommastellen genau!
Lösung:
Da f eine ganzrationale Funktion dritten Grades ist, hat f höchstens drei Nullstellen. Tatsächlich liegt eine davon im Intervall -3 ≤ x ≤ -2 und eine weitere im Intervall 2 ≤ x ≤ 3. Damit kann im Intervall 0 ≤ x ≤ 1 höchstens noch eine Nullstelle liegen.
Aus der Stetigkeit von f und aus f(0) = 13.75 > 0 sowie f(1) = -33.75 < 0 folgt, dass f irgendwo zwischen 0 und 1 den Wert Null annehmen muss. Im Intervall 0 ≤ x ≤ 1 liegt also genau eine Nullstelle von f.
Wir bestimmen nun auf numerischem Wege die Nullstelle aus dem Intervall -3 ≤ x ≤ -2 mit Hilfe des Newton-Verfahrens. Dazu benötigen wir noch die erste Ableitung von f:
f(x) = 8x3 – 55,5x + 13,75
f´(x) = 24*x2-55,5
Wir verwenden also die Iteration
und benutzen als Startwert x0 = -2,5 (die Mitte des Intervalls -3 ≤ x ≤ -2):
x0 = -2,5
x1 = -2,5 – f(-2,5) / f´(-2,5) = -2,79100529100529
x2 = -2,79100529100529 – f(-2,79100529100529) / f´(-2,79100529100529) = -2,75085260705122
x3 = -2,75085260705122 – f(-2,75085260705122) / f´(-2,75085260705122) = -2,75000038051623
Wir erhalten als Nullstelle im Intervall -3 ≤ x ≤ -2 den Wert x = -2,75.
Quelle: Die Aufgaben sind dem Buch Abitur 2000 – Prüfungsaufgaben mit Lösungen, STARK Verlag, 1999 entnommen.