oHiMi Aufgaben BLF 2015 Thüringen

(1)   Skizzieren Sie die Graphen der Funktionen f(x) = 4·cos(x) und g(x) = cos(x) + 4 im Intervall
0 ≤ x ≤ 2π.

 

Um die Graphen zu skizieren, orientieren wir uns am ’normalen‘ Kosinus.

Der Faktor 4 in der Funktion f streckt die Funktion in y-Richtung:

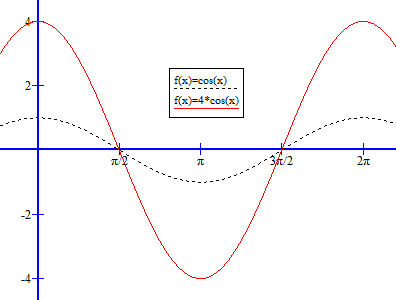
Tipp: Da die Schablone für sin/cos zugelassen ist, können wir sie natürlich hier auch benutzen. Wir müssen nur die y-Achse anstatt mit 1 und -1 mit 4 und -4 beschriften!

 

In der Funktion g wird zur cos-Funktion noch 4 dazuaddiert. Dies bewirkt eine Verschiebung in y-Richtung um 4 Einheiten nach oben:

(2)   Ein fünfstelliges Passwort soll nur aus ungeraden Ziffern bestehen, die alle verschieden sind. Wie viele mögliche Passwörter existieren?

 

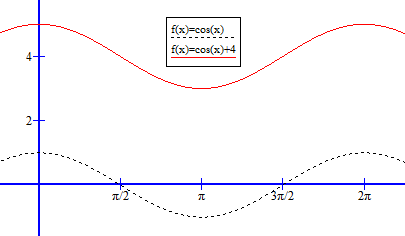
Für die erste Ziffer gibt es 5 Möglichkeiten (1, 3, 5, 7 oder 9).
Für die zweite Ziffer gibt es nur noch 4 Möglichkeiten, für die dritte nur noch 3, für die vierte nur noch 2 und für die fünfte und letzte Ziffer nur noch 1 Möglichkeit. Das sind insgesamt

5! = 5 · 4 · 3 · 2 · 1 = 120   mögliche Passwörter.

(3)   Das Ereignis E beschreibt alle Passwörter aus Aufgabe (2), die mit 1 anfangen. Das Ereignis F beschreibt diejenigen, die als Zahl gelesen durch 5 teilbar sind.

Welche der Passwörter (I) bis (V) gehören zum Ereignis E∩F ?
(I) 13579    (II) 13975    (III) 53791    (IV) 37915    (V) 17395

 

E∩F bedeutet E und F, also mit 1 beginnend und durch 5 teilbar. Dies trifft auf Passwort (II) und (V) zu.

(4)   Linus sagt die Gleichung 3x + c = -x² hat höchstens zwei Lösungen. Hat er recht, wie beeinflusst c die Lösungsmenge?

 

Rechnerische Lösung (mit pq-Formel):

3x + c = -x²

x² + 3x + c = 0

x_1,2 = -1,5 ± √( 2,25 – c )

2,25 – c > 0 bzw. c < 2,25 ⇒ 2 Lösungen 2,25 - c = 0 bzw. c = 2,25 ⇒ 1 Lösung 2,25 - c < 0 bzw. c > 2,25 ⇒ keine Lösung

Linus hat also recht.

 

Grafische Lösung (mit Parabelschablone):

Wir fassen die linke und die rechte Seite der Gleichung jeweils als eine Funktionen auf, die wir für verschiedene c zeichnen. Die Anzahl der Lösungen entspricht dann der Anzahl der Schnittpunkte der beiden Graphen:

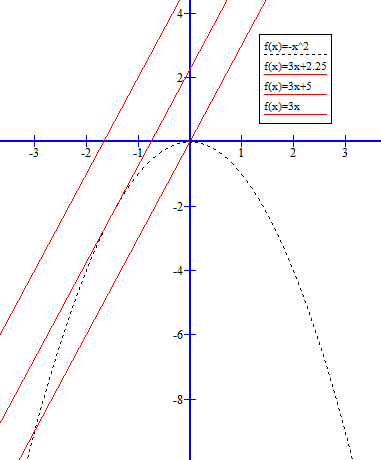
Auch hier sieht man, dass Linus recht hat.

(5)   In einem Dreieck ABC ist der Winkel α doppelt so groß wie Winkel β und 15° größer als Winkel γ. Wie groß sind die drei Winkel?

 

Wir lösen die Aufgabe mit Hilfe eines Gleichungssystems:

 

I     α = 2 · β

II    α = 15° + γ

III   α + β + γ = 180°

 

Aus I und II erhalten wir 2 · β = 15° + γ und daraus

 

IV   β = 7,5° + 0,5·γ

 

Aus II in III erhalten wir 15° + γ + β + γ = 180° daraus mit IV

 

15° + γ + 7,5° + 0,5·γ + γ = 180°

22,5° + 2,5·γ = 180°

2,5·γ = 157,5°

γ = 63°

 

Mit γ = 63° in II ergibt sich

α = 15° + 63° = 78°

und mit I erhalten wir noch β = 39°.

 

Für das betrachtete Dreieck gilt also α = 78°, β = 39° und γ= 63°.

(6)   Geben Sie zu dem folgenden rechtwinkligen Dreieck RST jeweils eine Gleichung zur Berechnung der Seite RS und des tan(∠RTS) unter Verwendung der Dreiecksseiten an.

 

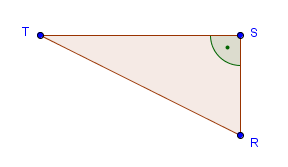
Für die Seite RS benutzen wir den Satz des Pythagoras RT² = RS² + ST² und erhalten

RS = √( RT² – ST² ).

 

Der Tangens eines Winkels ist gleich dem Verhältnis von Gegenkathete zu Ankathete. Der Winkel ∠RTS in unserem Dreieck hat seinen Scheitelpunkt bei T. Für diesen Winkel ist RS die Gegenkathete und ST die Ankathete. Wir erhalten also

tan(∠RTS) = RS / ST.