In diesem Beitrag wird erklärt wie man eine quadratische Funktion in Normalform in die entsprechende Scheitelpunktform umwandelt.
Zunächst erfolgt die Herleitung der Formel x2 + px + q = (x + p/2)2 – p2/4 + q und dann ihre Anwendung in vier Beispielen.
Herleitung der Formel:
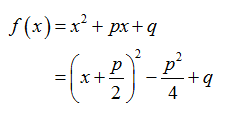
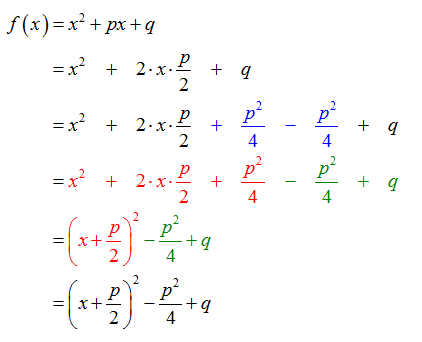
Der Scheitelpunkt lautet damit
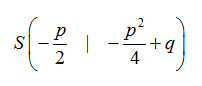
Hier nun ein ausführliches Beispiel für eine Umwandlung von der Normalform in die Scheitelpunktform:
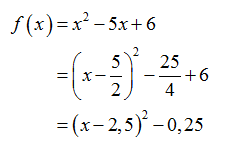
Drei weitere Beispiele in Kurzform:
f(x) = x2 – 8x + 15 = (x – 4)2 – 1
f(x) = x2 – 9x + 14 = (x – 4,5)2 – 6,25
f(x) = x2 + 10x – 13 = (x + 5)2 – 38