In diesem Beitrag geht es um die Rangbestimmung eines endlichen Systems von Vektoren mit Hilfe elementarer Umformungen.
Elementare Umformungen eines Systems von Vektoren
Jede der drei folgenden Aktionen nennt man eine elementare Umformung eines Vektorsystems v1, … , vm:
- Addieren eines skalaren Vielfachen avj des Vektors vj zum Vektor vi
- Vertauschen zweier Vektoren vi und vj
- Multiplizieren eines Vektors vi mit einem Skalar a ≠ 0
Geht das Vektorsystem v‘1, … , v‘m durch elementare Umformungen aus dem Vektorsystem
v1, … , vm hervor, so gilt: Rang(v‘1, … , v‘m) = Rang(v1, … , vm).
Geordnete Basis eines Vektorraums
Wir betrachten nun einen endlich erzeugbaren K-Vektorraum V. Ein solcher Vektorraum besitzt eine Basis der Form
und jeder Vektor v aus V ist eine Linearkombination
der Vektoren aus B mit eindeutig bestimmten Skalaren ai. Die Gestalt des Tupels (a1,…,an) ∈ Kn hängt von drei Dingen ab: vom Vektor v, von der Basis B und von der gewählten Numerierung der u1, … , un.
Beispiel: Sei V = IR2, v = (10,12), B = { (2,0), (0,2) }.
Dann ist einerseits v = (10,12) = 5·(2,0) + 6·(0,2) mit (a1,a2) = (5,6).
Andererseits ergibt sich durch eine Umnumerierung der Vektoren in B die Darstellung
v = (10,12) = 6·(0,2) + 5·(2,0) mit (a1,a2) = (6,5).
Daher spricht man auch bei Vektoren ui_1, … , ui_n von einer geordneten Basis, für jede feste Anordnung i_1,…,i_n der Zahlen 1 bis n und einer gegebenen Basis B = { u1, … , un }.
Koordinaten und Koordinatenvektor bezüglich einer Basis
Sei V ein K-Vektorraum, u1, … , un eine geordnete Basis von V und v ein beliebiger Vektor aus V.
Dann nennt man die eindeutig bestimmten Skalare ai ∈ K in der Darstellung
die Koordinaten von v bezüglich der Basis u1, … , un und (a1,…,an) ∈ Kn den Koordinatenvektor von v bezüglich der Basis u1, … , un.
Im Beispiel oben hat also der Vektor v = (10,12) einmal den Koordinatenvektor (5,6) und ein anderes mal den Koordinatenvektor (6,5) je nachdem, welche geordnete Basis man zugrunde legt.
(10,12) selbst ist Koordinatenvektor von v bezüglich der kanonischen Einheitsbasis (1,0), (0,1).
Koordinatenmatrix bezüglich einer Basis
Sei V ein K-Vektorraum, u1, … , un eine geordnete Basis von V und v1, … , vm ein System von Vektoren aus V. Dann heißt die m x n – Matrix
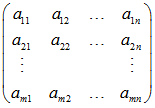
die Koordinatenmatrix von v1, … , vm bezüglich der Basis u1, … , un, wenn jede Zeile i
( i = 1,…,m ) der Matrix A dem Koordinatenvektor 
von Vektor vi
in der eindeutigen Darstellung 
bezüglich der Basis u1, … , un entspricht.
Elementare Umformungen auf ein System von Vektoren anzuwenden, ist dann völlig gleichbedeutend damit, elementare Zeilenumformungen mit einer Koordinatenmatrix dieser Vektoren durchzuführen.
Verfahren zur Rangbestimmung eines endlichen Systems von Vektoren
Sei V ein endlich erzeugbarer K-Vektorraum, u1, … , un eine (geordnete) Basis von V und v1, … , vm irgendein endliches System von Vektoren aus V. Man überführe die m x n – Koordinatenmatrix
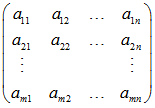
der Vektoren v1, … , vm in eine m x n – Matrix der Form
.Der blaue Teil in A‘ ist dann die r x r – Einheitsmatrix für ein gewisses r mit 0 ≤ r ≤ m,n und die unteren m – r Zeilen sind allesamt Nullzeilen.
Es ist stets möglich A in die Form A‘ zu bringen – in dem uninteressanten Fall, dass das System v1, … , vm aus lauter Nullvektoren besteht, ist dann natürlich A (und auch A‘) die m x n – Nullmatrix und somit r = 0.
Die Matrix A‘ steht für ein (Rang-gleiches) System von aus v1, … , vm hervorgegangenen Vektoren v‘1, … , v‘m bezüglich einer Basis u‘1, … , u‘n.
Dabei sind die u‘1, … , u‘n höchstens durch Umnumerierung aus der Basis u1, … , un hervorgegangen (was Spaltenvertauschungen in A entspricht).
Als Begründung hierfür kann man sich überlegen, dass
Rang( v1, … , vm ) = Rang( v‘1, … , v‘r, 0, … , 0 ) = r ist.
Beispiel für eine Rangbestimmung
Wir bestimmen den Rang des Vektorsystems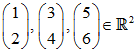 
. Als Basis wählen wir die kanonische Einheitsbasis 
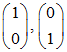. Damit erhält man die Koordinatenmatrix
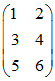
Man subtrahiert das 3-fache der ersten Zeile von der zweiten und erhält
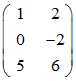
Man subtrahiert das 5-fache der ersten Zeile von der dritten und erhält
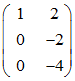
Man subtrahiert das 2-fache der zweiten Zeile von der dritten und erhält
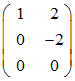
Genau genommen könnte man hier schon aufhören, da sich der Rang bereits jetzt ablesen lässt (In einer Software zur Rangbestimmung würde man – um Zeit und Speicher zu sparen – dies sicher auch so tun).
Wir wollen dieses kleine Beispiel aber mal vollständig zu Ende rechnen. Dazu multipliziert man als nächstes die zweite Zeile mit -1/2 und erhält
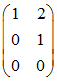
Subtrahiert man nun noch das 2-fache der zweiten Zeile von der ersten Zeile, kommt man auf die gewünschte Form
Wir stellen fest: Das gegebene System hat den Rang r = 2, denn die Matrix enthält die 2 x 2 – Einheitsmatrix, es gibt 3 – 2 = 1 Nullzeile, Spaltenvertauschungen waren nicht notwendig (die kanonische Einheitsbasis blieb unangetastet).