Eine Raute (Rhombus) ist ein Viereck, in dem alle Seiten gleich lang und gegenüberliegende Seiten parallel sind.
Die Diagonalen stehen senkrecht aufeinander und halbieren einander.
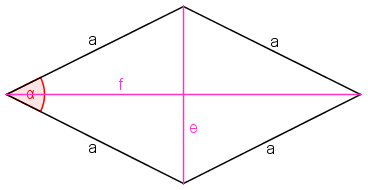
Der Umfang einer Raute ist
U = 4a
Beispiele:
Gegeben ist eine Raute mit der Seite a = 12cm.
Gesucht ist der Umfang der Raute.
Die Raute hat einen Umfang U = 4·12cm = 48cm.
Gegeben ist der Umfang einer Raute mit U = 36cm.
Gesucht ist die Seitenlänge a der Raute.
Aus U = 4a erhält man 36cm = 4·a.
Damit gilt für die gesuchte Seite: a = 36cm : 4 = 9cm.
Die Fläche (Flächeninhalt) einer Raute berechnet man durch
A = 1/2 ef = a2 sin α
Beispiele:
Gegeben ist eine Raute mit den Diagonalen e = 4cm und f = 2cm.
Gesucht ist der Flächeninhalt der Raute.
Es ist A = 1/2 ef = 1/2 · 4cm · 2cm = 4cm2.
Gegeben ist eine Raute mit der Seitenlänge a = 2,5cm
und einem Winkel α = 45°.
Gesucht ist der Flächeninhalt der Raute.
Es ist A = a2 sin α = (2,5cm)2 · sin 45° = 6,25cm2 · 0,7071 = 4,4194cm2.
Die Diagonalen e und f der Raute berechnet man mit Hilfe von
e2 = 4a2 – f2 bzw. f2 = 4a2 – e2
Beispiel
Gegeben ist eine Raute mit der Seitenlänge a = 9cm
und der Diagonale f = 12cm.
Gesucht ist die andere Diagonale e.
Es ist e2 = 4a2 – f2 = 4 · 81cm2 – 144cm2,
also e2 = 324cm2 – 144cm2 = 180cm2.
Damit gilt: e = √180cm2 = 13,4164cm.