Sind (an) und (bn) konvergente Folgen dann gilt:
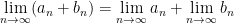
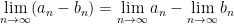
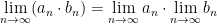
sofern die
und
ungleich Null.
Beispiele für die Verwendung der Rechenregeln:
Sind (an) und (bn) konvergente Folgen dann gilt:
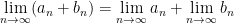
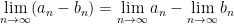
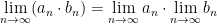
sofern die
und
ungleich Null.
Beispiele für die Verwendung der Rechenregeln: