Wir betrachten die Folge (an) mit an = n/(n + 1).
Ihre ersten Folgeglieder sind 1/2 , 2/3 , 3/4 , 4/5 , … , 99/100 , … .
Man sieht (oder weist es explizit nach), dass die Folge streng monoton wachsend aber gleichzeitig nach oben durch die Zahl 1 beschränkt ist.
Die Folgeglieder mit den Indizes 9, 99 und 9999 sind 9/10 , 99/100 und 9999/10000 und man erkennt leicht, dass sich diese Zahlen immer weiter und weiter der Zahl 1 annähern.
So ist der Abstand zwischen 1 und allen Folgegliedern ab Index 10 schon kleiner als
1/10 = 0,1 und der Abstand zwischen 1 und allen Folgegliedern ab Index 106 kleiner als 10-6=0,000001 usw.
Diese Eigenschaft von gewissen Folgen – nämlich, dass ’spätere‘ Folgeglieder immer ‚dichter‘ bei einer bestimmten Zahl g liegen (oder sogar mit g übereinstimmen) und sich auch nicht wieder von g ‚entfernen‘, führen zu den Begriffen Grenzwert und Konvergenz bei Zahlenfolgen:
Eine reelle Zahl g heißt Grenzwert (Limes) einer Folge (an), wenn zu jedem reellen ε>0 ein Index n0 existiert, sodass für alle natürlichen Zahlen n≥n0 die Beziehung
|an – g| < ε gilt.Jede Folge (an), die einen Grenzwert g besitzt, nennt man konvergent.
Man sagt dann die Folge (an) konvergiert gegen g und schreibt dafür:
Limes von an für n gegen unendlich ist gleich g oder
für
an strebt/konvergiert gegen g für n gegen unendlich.
Das ε in obiger Definition gibt den Abstand zur Zahl g vor. Es darf beliebig klein werden und trotzdem muss der Abstand aller Folgeglieder an zu g von einem gewissen n=n0 an immer noch kleiner sein als ε. Es darf sozusagen nur endlich viele Ausnahmen von Folgegliedern geben, die die Abstandsbedingung nicht einhalten.
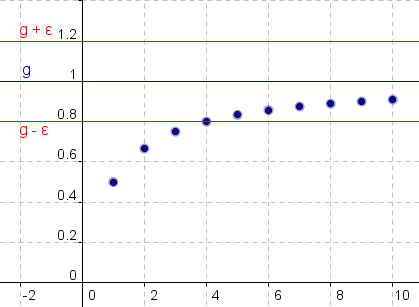
Man kann die letzte Bemerkung anhand des folgenden Bildes leicht nachvollziehen. Dort sind die ersten zehn Folgeglieder der Beispiel-Folge von oben – an = n/(n + 1) – in einem Diagramm dargestellt.
Im Bild wurde für ε der Wert 0,2 gewählt. Es entsteht damit um den Grenzwert g=1 ein ‚Streifen‘ der Breite 2ε=0,4 und innerhalb dieses Streifens liegen alle Folgeglieder ab Folgeglied a5=5/6 (das sind unendlich viele – ohne jegliche Ausnahme!).
Der besagte Index aus der Definition, von dem ab für das gewählte ε=0,2 die Abstandsbedingung erfüllt ist, ist also n0=5.
Wie weist man nun aber nach, dass eine vorgelegte Folge konvergent ist – also einen Grenzwert besitzt?
Solange man nur die obige Definition zur Verfügung hat (und sonst keine weiteren Konvergenzkriterien), bleibt einem nichts weiter übrig als einen Grenzwert g zu raten und dann zu versuchen Diesen mittels sogenannter Epsilontik als Grenzwert nachzuweisen.
Beispiel:
Wir betrachten nochmal die Folge (an) mit an = n/(n + 1). Die Berechnung der ersten Folgeglieder und das Bild-Beispiel von oben, lassen uns annehmen, dass g=1 der Grenzwert dieser Folge ist.
Wir setzen nun n/(n + 1) anstelle von an und den Wert 1 anstelle von g in die Abstandsbedingung aus der Definition ein und versuchen mit Äquivalenzumformungen nach n umzustellen:
| |an – g| < ε | |
| bedeutet hier | |n/(n + 1) – 1| < ε |
| ⇔ | |n/(n + 1) – (n + 1)/(n + 1)| < ε |
| ⇔ | |(n – n – 1)/(n + 1)| < ε |
| ⇔ | |-1/(n + 1)| < ε |
| ⇔ | 1/(n + 1) < ε |
| ⇔ | 1/ε < n + 1 |
| ⇔ | 1/ε – 1 < n |
An dieser Stelle sind wir fertig. Die letzte Ungleichung sagt uns, dass wir für ein beliebig vorgegebenes ε>0 für die zugehörige Indexzahl n0 eine natürliche Zahl zu wählen haben, die größer ist als 1/ε – 1 und von da an (also für alle n≥n0) ist die Abstandsbedingung für die Folgeglieder an erfüllt.
Laut Definition ist damit g=1 als Grenzwert der vorgelegten Folge nachgewiesen ◊