Auf dieser Seite gibt es für euch Geometrie/Algebra – Mathe Abituraufgaben mit Lösungen und zwar den Teil B2, Aufgabe e und f (Sachsen 1994).
Gegeben:
In einem kartesischen Koordinatensystem sind folgende Punkte gegeben:
A = (2; 2; -2)
B = (4; -4; 2)
C = (8; 2; 2)
D = (6; 8; -2)
Aufgabe e)
Das Viereck ABCD ist ein Parallelogramm.
Die Diagonale AC von ABCD schneidet die x-y-Ebene in einem Punkt S.
Es sind die Koordinaten von Punkt S zu berechnen und es ist zu zeigen, dass S der Schnittpunkt der Diagonalen im Parallelogramm ABCD ist!
Lösung:
Da der Punkt S = (xS; yS; zS) in der x-y-Ebene liegt, muss zS = 0 gelten. Außerdem muss er auf der Geraden
x = →
OA + α·→
AC
liegen. Aus beiden Bedingungen zusammen erhält man die Koordinaten vom Punkt S:
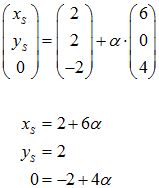
Aus der unteren Gleichung erhalten wir α = 0,5. Dies eingesetzt in die erste Gleichung ergibt xS = 5 und yS lässt sich von vornherein ablesen: yS = 2.
Somit hat der gesuchte Schnittpunkt S mit der x-y-Ebene die Koordinaten (5; 2; 0).
Um zu zeigen, dass S auch der Schnittpunkt der beiden Diagonalen AC und BD ist, kann man so vorgehen:
Die Diagonalen in einem Parallelogramm halbieren sich bekanntlich. Demnach reicht es, den Mittelpunkt einer der Diagonalen zu berechnen. Sollte dieser mit dem Punkt S übereinstimmen, so ist S als Schnittpunkt der Diagonalen nachgewiesen.
Wir berechnen den Mittelpunkt der Diagonalen BD:
M = ( (4+6)/2 ; (-4+8)/2 ; (2-2)/0 ) = (5; 2; 0)
Da dies die gleichen Koordinaten sind wie die von S, ist S tatsächlich der Schnittpunkt der Parallelogramm-Diagonalen.
Aufgabe f)
Die Gerade g mit
OS
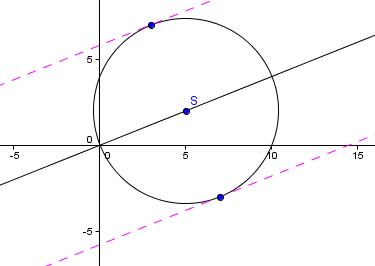
geht durch den Koordinatenursprung sowie den Punkt S.
Der Kreis k mit Mittelpunkt S und Radius r = √29
liegt in der x-y-Ebene.
Zu bestimmen sind die Gleichungen aller Tangenten an den Kreis k, die parallel zur Geraden g verlaufen!
Lösung:
Von den zu bestimmenden Tangenten kann es nur zwei geben und wir wissen, dass beide den Anstieg m = 2/5 haben müssen, da
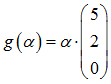
in der x-y-Ebene liegt und sich kurz und knapp durch y = 2/5·x ausdrücken lässt.
Was wir noch nicht wissen, sind die beiden Stellen an denen die besagten Tangenten unseren Kreis berühren. Um diese zu finden, berechnen wir die Normale zu y = 2/5·x:
yN – yS = -m · (x – xS)
yN – 2 = -5/2 · (x – 5)
yN – 2 = -5/2·x – 5/2·(-5)
yN = -5/2·x – 5/2·(-5) + 2
Senkrecht zu y = 2/5·x und durch S = (5; 2; 0) verläuft also
Die Berührungspunkte mit dem Kreis ermitteln wir so:
Für einen Punkt auf dem Kreis muss gelten
(x – 5)2 + (y – 2)2 = 29 bzw. (y – 2)2 = 29 – (x – 5)2 .
Für einen Punkt auf der Normalen muss gelten
yN = -5/2·x + 14,5 bzw. (yN – 2)2 = (-5/2·x + 12,5)2 .
Wir erhalten hieraus durch Gleichsetzen
29 – (x – 5)2 = (-5/2·x + 12,5)2
4 – x2 + 10x = 6,25x2 – 62,5x + 156,25
0 = 7,25x2 – 72,5x + 152,25
0 = x2 – 10x + 21
mit den beiden Lösungen x1 = 7 und x2 = 3.
Setzt man diese beiden Werte in die Normalengleichung ein, so ergeben sich die folgenden Berührungspunkte mit dem Kreis:
Damit lauten die beiden gesuchten Tangenten
yt2 – 7 = 2/5·(x – 3) bzw. yt2 = 2/5·x + 5,8
Quelle: Die Aufgaben sind dem Buch Abitur 2000 – Prüfungsaufgaben mit Lösungen, STARK Verlag, 1999 entnommen.