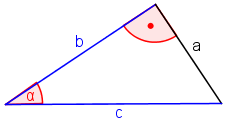
Der Cosinus eines spitzen Winkels α im rechtwinkligen Dreieck ist definiert als das Verhältnis von Ankathete von α zu Hypotenuse:
cos α = b / c
Beispiel:
In einem rechtwinkligen Dreieck mit der Hypotenuse c = 5cm hat der Winkel α eine Ankathete b = 4cm. Gesucht ist Cosinus von α und α selbst!
Es ist cos α = 4/5 und damit α = cos-1 4/5 ≈ 36,9°.
Mit dem Seitenverhältnis 4/5 lässt sich mit Hilfe der Umkehrfunktion vom Cosinus (Arkuscosinus, auf dem Taschenrechner meist cos-1) der Winkel berechnen!
Aus der obigen Formel für den Cosinus kann man aus dem Winkel α und einer der beiden Seiten die jeweils andere Seite berechnen:
c = b / cos α
Beispiel:
In einem rechtwinkligen Dreieck mit α = 55° und Hypotenuse c = 8cm ist die Ankathete von α: b = c · cos α = 8cm · cos 55° ≈ 4,59cm.
Für die Grenzfälle α = 0° bzw. α = 90° ist festgelegt:
cos 0° = 1
cos 90° = 0