Geometrie, Algebra – Mathe Abituraufgaben mit Lösungen – Sachsen 1994 (B1 c,d)

Auf dieser Seite gibt es für euch Geometrie/Algebra – Mathe Abituraufgaben mit Lösungen und zwar den Teil B1, Aufgabe c und d (Sachsen 1994).

Gegeben:

Punkte A = (7; -5; 0), B = (2; 0; 0) und C = (2; -6; 0) sowie eine Gerade g durch die folgende Gleichung
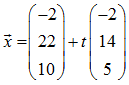
Gerade g

Aufgabe c)

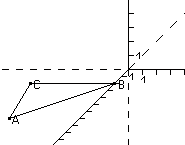
Zu bestimmen sind die Geradengleichungen der drei Mittelsenkrechten des Dreiecks ABC sowie die Koordinaten des Schnittpunkts M der Mittelsenkrechten!
Dreick ABC in x-y-Ebene

Lösung:

Der Mittelpunkt zwischen Punkt A und Punkt B liegt bei

( (7 + 2)/2 ; (-5 + 0)/2; (0 + 0)/2 ) = (4,5; -2,5; 0) .

Die Gerade, auf der die Mittelsenkrechte der Strecke AB liegt, verläuft durch diesen Punkt in orthogonaler Richtung zum Vektor
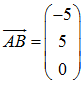
Vektor AB

Orthogonal hierzu ist z.B. der Vektor
Vektor (5, 5, 0)

Damit lautet die Geradengleichung der Mittelsenkrechten der Strecke AB
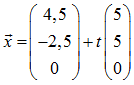
Gerade mAB

Auf entsprechende Weise findet man die Geradengleichung der Mittelsenkrechten der Strecke BC
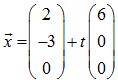
Gerade mBC

und die Geradengleichung der Mittelsenkrechten der Strecke AC
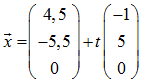
Gerade mAC

Um den Schnittpunkt M zu berechnen, benutzen wir die letzten beiden Geraden. Es muss zwei Zahlen t1 und t2 geben, sodass folgendes gilt:
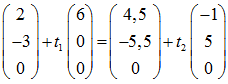
Schnittpunktberechnung

In der mittleren Gleichung kommt nur t2 vor:

-3 = -5,5 + 5t2

woraus man t2 = 0,5 erhält. Mit dieser Zahl und der letzten Geradengleichung ergibt sich

4,5 + 0,5 · (-1) = 4

-5,5 + 0,5 · 5 = -3

0 + 0,5 · 0 = 0

Der Schnittpunkt M hat also die Koordinaten (4 ; -3 ; 0).

Man sieht sofort (t = -0,1), dass Punkt M auch zur ersten Geraden gehört:
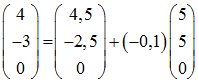
Proberechnung

Aufgabe d)

Der in Aufgabe c) berechnete Punkt M ist der Mittelpunkt des Umkreises von Dreieck ABC. Zu bestimmen ist nun die Gleichung dieses Kreises!

Lösung:

Genau wie das Dreieck und der Punkt M liegt besagter Kreis in der x-y-Ebene und lässt sich damit durch eine Gleichung der Form

(x – xM)2 + (y – yM)2 = r2

beschreiben. Hierin ist xM = 4 und yM = -3, also die x- und die y-Koordinate von Punkt M.

Was noch fehlt ist der Radius r des Umkreises, also der Abstand von M zu einem der Punkte A, B oder C. Wir berechnen ihn mit Hilfe von A

r = √( (xM – xA)2 + (yM – yA)2 )

r = √( (4 – 7)2 + (-3 – (-5))2 ) = √( 9 + 4 ) = √13

Damit ist (x – 4)2 + (y + 3)2 = 13 die gesuchte Kreisgleichung.

Quelle: Die Aufgaben sind dem Buch Abitur 2000 – Prüfungsaufgaben mit Lösungen, STARK Verlag, 1999 entnommen.

Auch interessant: