Auf dieser Seite gibt es für euch Geometrie/Algebra – Mathe Abituraufgaben mit Lösungen und zwar den Teil B2, Aufgabe a und b (Sachsen 1994).
Gegeben:
In einem kartesischen Koordinatensystem sind folgende Punkte gegeben:
A = (2; 2; -2)
B = (4; -4; 2)
C = (8; 2; 2)
D = (6; 8; -2)
Aufgabe a)
Es ist nachzuweisen, dass das Dreieck ABC gleichschenklig ist und es ist seine Basis und einer der Basiswinkel zu berechnen!
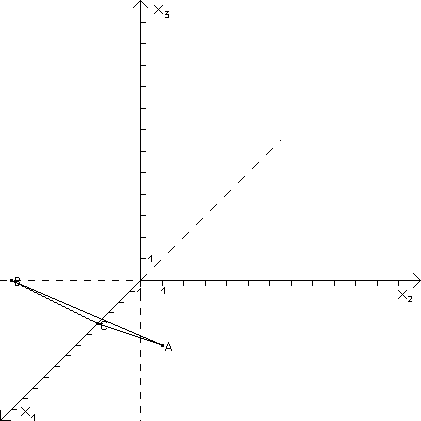
Lösung:
Das Dreieck ABC ist genau dann gleichschenklig, wenn es wenigstens zwei gleichlange Seiten gibt. Wir berechnen also zunächst die Länge der drei Seiten des gegebenen Dreiecks:
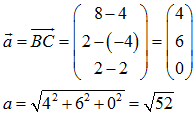
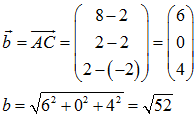
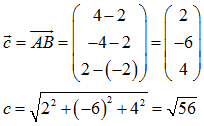
Strecke BC (also Seite a) und Strecke AC (d.h. Seite b) sind also gleich lang und damit ist Dreieck ABC tatsächlich gleichschenklig.
Die Basis dieses Dreiecks ist die Seite c und es ist c = √56 = 7,48331.
Jetzt benötigen wir noch einen der beiden Basiswinkel α oder β. Wir entscheiden uns für β und berechnen ihn mit Hilfe des Skalarproduktes →
BA · →
BC:
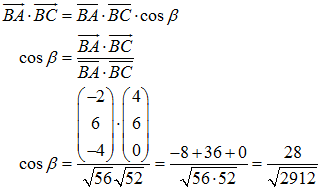
d.h. der Basiswinkel β beträgt cos-1(28/√2912) = 58,7°.
Aufgabe b)
Es ist festzustellen, ob die Vektoren →
AB und →
BD senkrecht zueinander stehen!
Lösung:
Für diese Aufgabe müssen wir das Skalarprodukt der beiden Vektoren berechnen. Ist es Null, so stehen die Vektoren senkrecht zueinander.
Den Vektor →
AB haben wir schon weiter oben berechnet. Er lautet
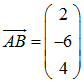
Der Vektor →
BD hat die folgende Gestalt:
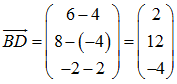
Das Skalarprodukt lautet:
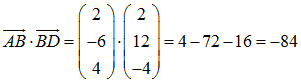
d.h. die beiden Vektoren sind nicht senkrecht zueinander.
Quelle: Die Aufgaben sind dem Buch Abitur 2000 – Prüfungsaufgaben mit Lösungen, STARK Verlag, 1999 entnommen.