Auf dieser Seite gibt es für euch Geometrie/Algebra – Mathe Abituraufgaben mit Lösungen und zwar den Teil B2, Aufgabe c und d (Sachsen 1994).
Gegeben:
In einem kartesischen Koordinatensystem sind folgende Punkte gegeben:
A = (2; 2; -2)
B = (4; -4; 2)
C = (8; 2; 2)
D = (6; 8; -2)
Aufgabe c)
Gesucht ist eine Gleichung der Ebene E, in welcher die drei Punkte A, B, C liegen! Liegt auch Punkt D in dieser Ebene?
Lösung:
Die vektorielle Drei-Punkte-Form der gesuchten Ebene lautet
x = →
OA + α·→
AB + β·→
AC.
Wir berechnen hierzu die drei beteiligten Vektoren:
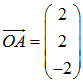
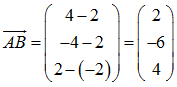
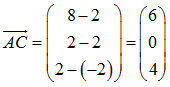
Somit lautet die gesuchte Gleichung für die Ebene E
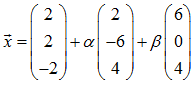mit reellen Zahlen α, β.
Um zu prüfen, ob auch der Punkt D = (6; 8; -2) in der Ebene E liegt, müssen wir ermitteln, ob es Zahlen α und β gibt, sodass gilt:
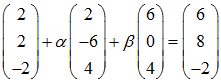
Wir haben also obiges Gleichungssystem zu lösen und nehmen dazu noch einige Umformungen vor:
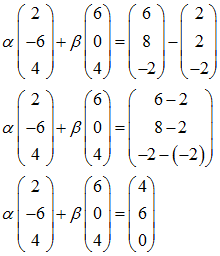
Hieraus erhalten wir die folgenden drei Gleichungen
2 α + 6 β = 4
-6 α = 6
4 α + 4 β = 0
Aus der mittleren Gleichung erhalten wir α = -1 und aus der oberen (oder unteren) Gleichung bekommt man durch Einsetzen von α = -1 für β den Wert β = 1.
Der Punkt D kann also mit Hilfe der Ebenengleichung ausgedrückt werden,
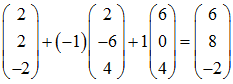d.h. D ist ebenfalls ein Punkt in der Ebene E.
Aufgabe d)
Gesucht sind die Koordinaten xF und zF eines Punktes F = (xF; -4; zF), sodass das Viereck ABFC ein Parallelogramm ist!
Lösung:
Aus der folgenden Skizze kann man die Lösungsidee ableiten:
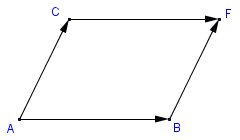
Es muss →
AC = →
BF und →
AB = →
CF gelten.
Mit den Koordinaten von A, B, C und yF = -4 erhält man hieraus
→
AC = →
BF
| 8 – 2 = xF – 4 | → | xF = 10 |
| 2 – 2 = -4 + 4 | → | 0 = 0 |
| 2 + 2 = zF – 2 | → | zF = 6 |
und
→
AB = →
CF
| 4 – 2 = xF – 8 | → | xF = 10 |
| -4 – 2 = -4 – 2 | → | -6 = -6 |
| 2 + 2 = zF – 2 | → | zF = 6 |
Der gesuchte Punkt F hat die Koordinaten (10; -4; 6).
Quelle: Die Aufgaben sind dem Buch Abitur 2000 – Prüfungsaufgaben mit Lösungen, STARK Verlag, 1999 entnommen.