Höhensatz des Euklid

In jedem rechtwinkligen Dreieck bezeichnet man die Seite, die dem rechten Winkel gegenüberliegt als Hypotenuse und die beiden anderen Seiten als Katheten. Ist c die Hypotenuse, sind a, b die Katheten und fällt man die Höhe h vom Punkt C auf die Seite c, so wird c aufgeteilt in zwei Hypotenusenabschnitte p und q. Der sogenannte Höhensatz des Euklid lautet dann

$h^2 = p \cdot q$

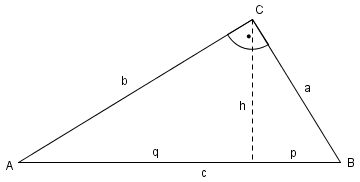Das Dreieck ABC wird durch die Höhe h zerlegt in zwei rechtwinklige Teildreiecke, jeweils ruhend auf einem der Hypotenusenabschnitte p bzw. q. Hat man nur Informationen über p und q, so lässt sich nun die Höhe im ‚großen‘ Dreieck ermitteln. Hat man dagegen Informationen über h und einen der Abschnitte, so kann man den jeweils anderen Abschnitt berechnen und aus beiden Abschnitten schließlich die Grundseite von Dreieck ABC (da c=p+q):

geg.: $p,q$ ges.: $h$ Lsg.: $h^2 = p \cdot q$ $h = \sqrt{p \cdot q}$	geg.: $p=1\frac{4}{5}cm,q=3\frac{1}{5}cm$ ges.: $h$ Lsg.: $h^2 = 1\frac{4}{5}cm \cdot 3\frac{1}{5}cm$ $h = \sqrt{\frac{144}{25}cm^2} = \frac{12}{5}cm = 2\frac{2}{5}cm$
geg.: $h,p$ ges.: $q$ Lsg.: $q = \frac{h^2}{p}$	geg.: $h=2\frac{2}{5}cm,p=1\frac{4}{5}cm$ ges.: $q$ Lsg.: $q = \frac{(2\frac{2}{5}cm)^2}{1\frac{4}{5}cm}$ $q = \frac{16}{5}cm = 3\frac{1}{5}cm$
geg.: $h,q$ ges.: $p$ Lsg.: $p = \frac{h^2}{q}$	geg.: $h=2\frac{2}{5}cm,q=3\frac{1}{5}cm$ ges.: $p$ Lsg.: $p = \frac{(2\frac{2}{5}cm)^2}{3\frac{1}{5}cm}$ $p = \frac{9}{5}cm = 1\frac{4}{5}cm$