Zu bestimmen sind folgende, spezielle Sinuswerte: sin 30°, sin 60° und sin 45°. Die Herleitung der Werte erfolgt mit Hilfe spezieller geometrischer Figuren.
sin 30°
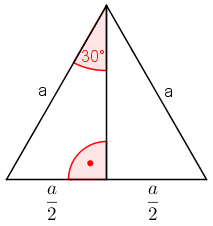
In diesem gleichseitigen Dreieck entsteht ein 30°-Winkel durch das Einzeichnen einer Höhe. Dadurch wird das Dreieck in zwei rechtwinklige Dreiecke zerlegt und die Grundseite halbiert. Man stellt fest:
Gegenkathete vom 30°-Winkel ist a/2
Hypotenuse ist a
sin 30° = (a/2)/a
sin 30° = 1/2.
sin 60°
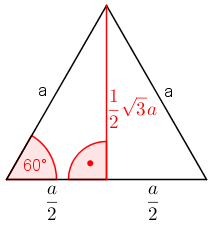
Wir bleiben in dem gleichseitigen Dreieck von oben. Der Winkel unten links beträgt natürlich 60° und die Höhe (rot) lässt sich mit dem Satz des Pythagoras berechnen, h2 = a2 – (a/2)2 = 4a2/4 – a2/4 = 3a2/4, also h = ½·√3·a.
Man errechnet: sin 60° = ½·√3·a / a = ½·√3.
sin 45°
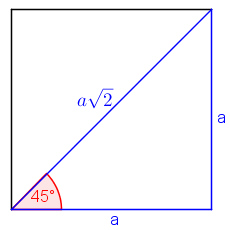
In obigem Quadrat entsteht durch Einzeichnen einer Diagonale ein 45°-Winkel in einem rechtwinkligen Dreieck. Berechnet man die Diagonale wieder mit Pythagoras, so ergibt sich:
Gegenkathete vom 45°-Winkel ist a
Hypotenuse ist a·√2
sin 45° = a / (a·√2) = 1 / √2 = √2 / (√2·√2), also
sin 45° = √2/2.